GeoMaestro
Projectors: reference
See this page for details about what exactly is a projector
All projectors are eventually based on the two fundamental ones:
Ecoute, EcouteS
Ecoute(A, B, ...)
A, B: points
EcouteS(Seg, ...)
Seg: segment
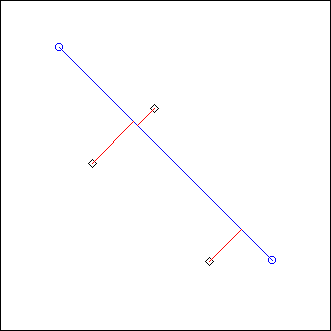
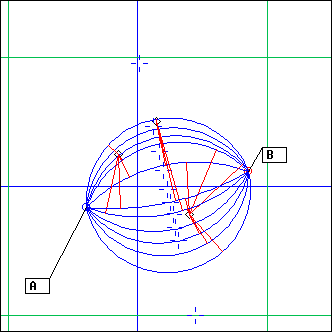
Ecoute() simply performs a projection on a segment defined by its starting point A and ending point B.
The principle of projection is explained here, along with a complete discussion on the way Ecoute() and EcouteC() work.
The optional (...) arguments are duration, t0, region and df:
duration: float
t0: integer
region: region
df: array
These optional arguments are the same for all projectors:
- duration sets the way duration is calculated from the length of the supports. See here for more (by default it is the length scaled by CPCM)
- t0 sets the starting time of the resulting phrase/ligne (by default it's 0)
- region sets the subset of events that will actually be projected, other events being ignored (by default it's the whole scene)
- df gives alternate distortion functions; its format and usage are detailed here
EcouteC
EcouteC(C, D, nT, ...)
C: circle
D: point or angle (float from 0 to 2*Pi)
nT: integer
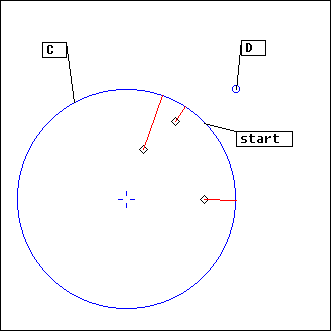
Projection is performed on circle C. Note that the center point, which logically should be projected everywhere on the circle, is ignored: an event at the center will be silent.
D is used to set the starting point on the circle: it will be where the line going through D and the center of C cuts the circle. So D doesn't have to belong to C. You can also directly give an angle value instead of a point.
nT is the number of rounds performed. Default sense of rotation is clockwise, but if nT is less than 0 it will be counter-clockwise
(Note that while Ecoute() listens to a subset of the event scene (precisely: the events in the ribbon defined by all segments that are a translation of AB along perpendicular vectors), EcouteC() listens to all events. The projector EarWalk makes use of this property by condensating the whole scene into a single point; this is a very interesting way to work with the distortion functions.)
An event at the same angle as the starting point will be projected at the very beginning, regardless of the rotation sense; it is not projected again at the end.
The projector ArcC makes it possible to use only a part of the circle as support.
Spiro
L = Spiro(C, radius, nT, theta0, dtheta, nC, D, ...)
nT, nC: integers
radius, dtheta, theta0: floats
C: circle
D: point or angle (float from 0 to 2*Pi)
ex: dtheta = 0.2*Pi, nC = 10
ex: dtheta = 0.3*Pi, nC = 10
EcouteC() is called for nC circles of radius radius whose centers belong to a circle C. The first circle's center is at angle theta0, the angle between two consecutive centers being dtheta. D is the starting point for EcouteC(). nT gives the sense of rotation (positive for clockwise) and the number of rounds along each circle.
Note: angle values always range from 0 to 2*Pi
Onde
L = Onde(C1, C2, nC, s, D, ...)
C1, C2: circles
nC, s: integers
D: point or angle (float from 0 to 2*Pi)
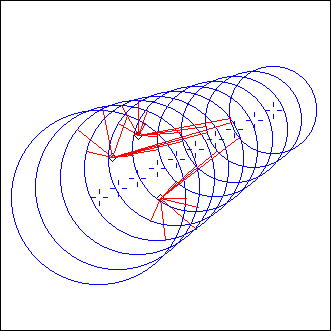
EcouteC() is called for nC circles evenly distibuted from C1 to C2. s is the sense of rotation (1 or -1) and D the starting point, for each circle.
Echelle
L = Echelle(A1, A2, B1, B2, nS, ...)
A1, A2, B1, B2: points
nS: integer
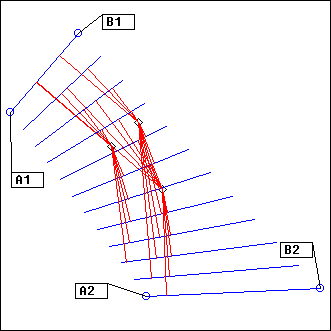
Ecoute() is called for nS segments evenly distributed from (A1 to B1) to (A2 to B2).
Helice
L = Helice(A, radius, theta0, dtheta, s, ...)
A: point
radius, theta, theta0: floats
s: integer
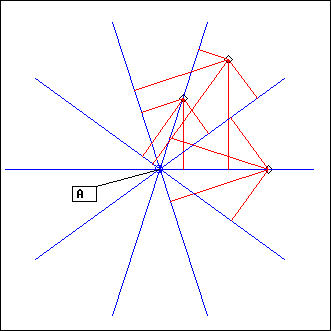ex: theta = 0, dtheta = 0.2*Pi
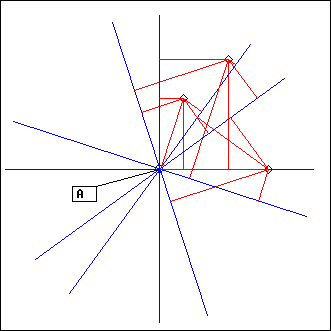ex: theta = 0, dtheta = 0.3*Pi
Ecoute() is called on segments turning around their middle point A. Segments length is 2*radius and the angle between two consecutive segments in dtheta. The fist segment is at angle theta0. s is the sens of rotation (1 or -1).
(see tutorial 1 for an example)
Brown
L = Brown(A, B, amplitude, lasting, {region,} ...)
A, B: points
amplitude: float
lasting: integer
region: region
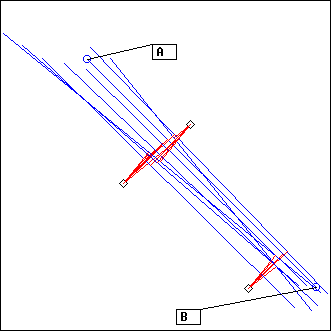
Ecoute() is called for as many segments as is necessary to obtain a rendered phrase of duration lasting. The first segment is AB, then A and B are randomly moved by a distance amplitude (Brownian diffusion), so that we get the next segment, and the process is repeated for each new segment.
The motion of the points A and B can be restricted to a geometrical region (optional argument. Note: if you need to give this argument only because you need to access the next optional ones, use the value Tout which is [0=0], the region covering everything. See data structures for the format of regions.)
AversB
L = AversB(A, B, length, theta, ...)
A, B: points
length: integer
theta: float
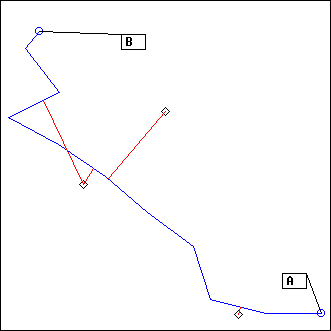ex: theta = 2
Ecoute() is called on segments whose length is length. We start from point A, ang go toward B. At each step, the direction taken is randomly choosen around the right direction, within a range of theta (in other words, it is the right direction plus a number from -theta/2 to theta/2)
The last segment is drawed then we got close enough to B, so its length is shorter than length.
Vague
L = Vague(P1, P2, length, theta, ...)
P1, P2: piste
length, theta: integer
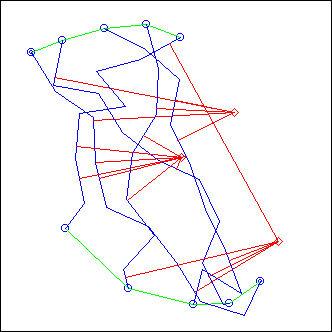ex: length = 0.2, theta = 2
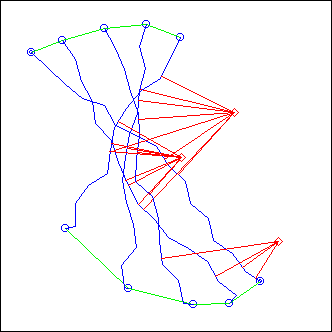ex: length = 0.1, theta = 1
Vague() is a kind of mixure of Echelle() and AversB():
AversB() is called for points in P1 to points in P2. In the example pictures, P1 is the piste formed by the five upper points (from left to right) and P2 the piste formed by the five lower points (from right to left)
Note that: Vague(P1, P2, length, theta)
... can be replaced by a MetaRails call: MetaRails(P1, P2, "AversB(A_,B_)")
CercleRythm
L = CercleRythm(A, B, nS, ...)
A,B: points
nS: integer
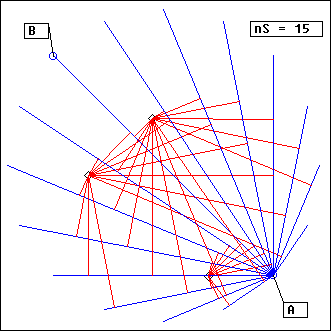
This projector is a very specific one, intended to generate interesting rythms. It is also the only one here that use the absolute mode for the duration parameter in Ecoute()
Ecoute() is called on a set of nS segments all starting at point A. The duration parameter is set according to the length of the segment AB. Segments are calculated so that A and B are always the first and last points that are projected onto them. Geometrically, it means that, since they all start at A, their other extremity is on the circle of diameter AB. The projector evenly distribute them on that circle
The way we handle duration here implies that all events on the segment AB will be rendered with the same time pattern for every segment. So if there are only events on that diameter segment, the result would be the same as repeating nS times Ecoute(A,B), apart from possible distortion effects coming from the distance/side changes. This gives a constant rythmic basis. Others events elsewhere in the scene may sound at very different times (or not sound at all !).
Scint
L = Scint(A, B, length, theta, n, ...)
A, B: points
theta: float
length, n: integers
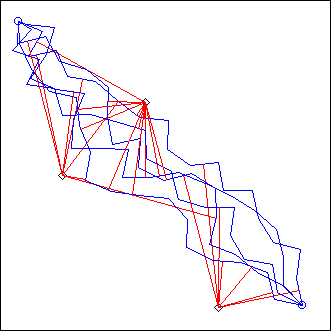
This is simply AversB() called n times...
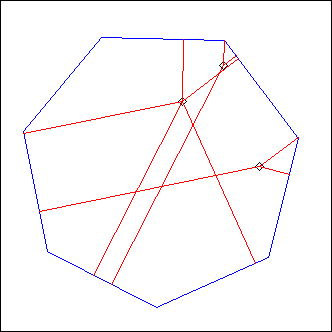
LSeq
L = LSeq(A, B, C, program)
A,B,C: points
program: string
(no usual optional arguments, only a closure)
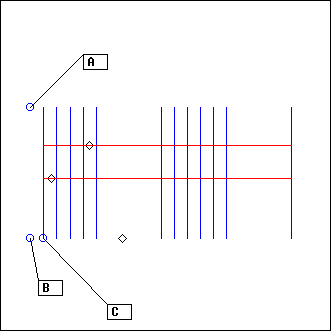
This is a rather ambitious projector, extending the linear sequencer described in tutorial 3.
The three points A,B,C design the geometry of an ordered collection of segments: segment number n will be parallel to AB and away from it by n times BC (in the example picture, you can see segments number 1,2,3,4,5,10,11,12,13,14,15 and 20)
program defines which segments will be listened to and in what order. "listen to" here means that Ecoute() will be called on the segment, with an automatic region parameter such that only the events in a rectangular region of width BC centered on the segment will be projected.
In other words, only events "close to" a segment are projected on this segment; and they are not be projected on any other segment (in the example picture, for example, corresponding to the program "1-5,10-15,20", the event at the right is ignored, the two other ones being projected respectively on segment 2 and on segment 4)
program syntax:
- segment numbers must be separated by commas
- n-p include segments n to p
- n_p means n times segment p
- n_p-q means n times the sequence of segments p to q
So, for example,
program = "10_5-10, 5_10-5, 1"
... loops 10 times the segments 5 to 10, then loops 5 times the segments 10 to 5, then plays segment 1.
The "LSeqCopy" plug-in is supposed to be used with an horizontal LSeq (like in the example picture). Check that the variable LSeqCopyDX is set to the distance between B and C. Then, you can copy an event from a line of the sequencer to the previous or next ones by clicking on the event and dragging the mouse: events will be created along this segment.
CSeq
L = CSeq(C, D, nT, program)
C: circle
D: point or angle (float from 0 to 2*Pi)
nT: integer
program: string
(no usual optional arguments, only a closure)
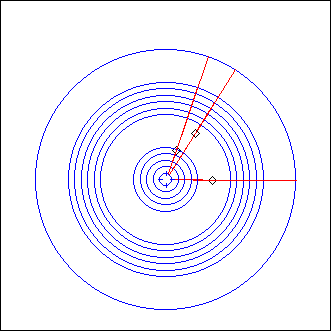
This is the circular sequencer detailled in tutorial 3, adapted as a projector.
C is the first circle: circle number n will have the same center and a radius n times bigger than C's.
D is the starting point for the circles, and nT their rotation parameter (see EcouteC() for details)
program is exactly the same as used with LSeq.
MetaRails
L = MetaRails(PA_, PB_, projcall)
PA_,PB_: pistes (or arrays of pistes)
projcall: string
(no usual optional arguments, only a closure)
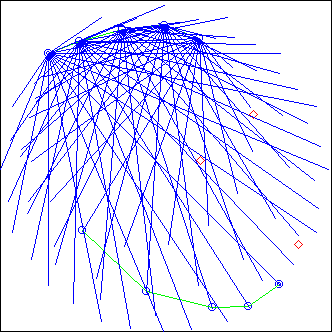
This is a meta-projector, that is: a projector calling another one.
It can be used with any projector taking (directly or not) points as arguments. projcall should be the complete call for this projector, using A_ and B_ for points arguments: the piste PA_ will provide the points A_, PB_ will provide the points B_
On the example picture, we used the same pistes from the example in Vague, while calling the projector CercleRythm:
projcall = "CercleRythm(A_,B_,15)"
Here's a second example, with
projcall = "Onde(Cerc(A_,0.1),Cerc(B_,0.1),10,1,ZOi)"
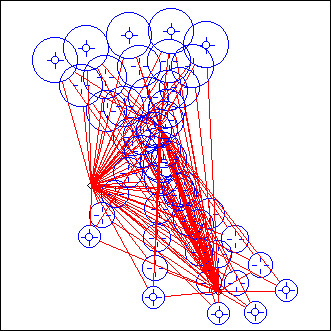
(as an extension, it is possible to provide arrays of pistes for A_ and B_, allowing projcall to refer to piste arguments. the indexes must then range from 1 to the number of pistes, index 0 being ignored if it exists. MetaPars provides a more general approach)
MetaPars
L = MetaPars(projcall, n, ...)
projcall: string
n: integer
... : any number of arrays or functions
(no usual optional arguments, only a closure)
This is another meta-projector, more general-purpose than Metarails
projcall should be the complete call for any projector, using P1_ ,P2_, ... as keywords for the following arguments. These arguments should be arrays or functions; projcall will be evaluated n times, the argument number i in call number m being Pi_[m] (if an array) or Pi_(m) (if a function)
For example, the illustration above comes from the following commands:
Projcall = "Arc(C1, P1_, P2_)"
Pos = []; for (i=1; i<=20; i++) Pos[i] = i<=10 ? 0: Pi
L = MetaPars(Projcall, 20, sin, Pos)
... in this example Projcall is evaluated for m =1 to 20, "P1_" being replaced by "sin(m)" and "P2_" being replaced by "Pos[m]"
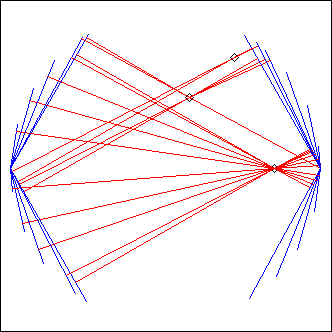
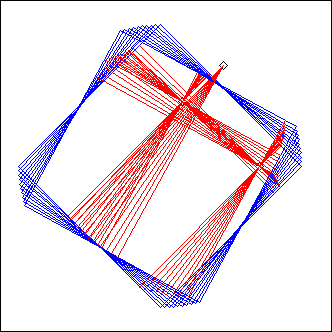
TDiam
L = TDiam(C, theta0, deltath, nT, projcall)
C: circle
theta0, deltath: float
nT: integer
projcall: string
(no usual optional arguments, only a closure)
TDiam stands for "T"urning "Diam"eter: it's an extension of the Helice principle.
theta0, deltath, nT have the same meaning as in Helice, while C replaces Helice's A and radius; but instead of calling Ecoute() on the parametric diameter, we call whatever projcall defines, using MetaRails
In the example picture, projcall was
projcall = "AversB(A_,B_,0.1,1)"
Arc
L = Arc(C, d, theta0, ...)
C: circle
d, theta0: float
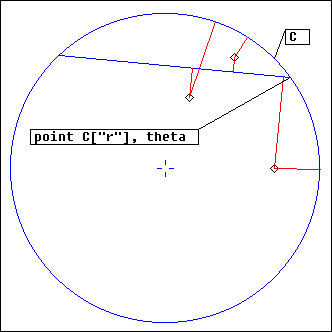
Ecoute() is performed on a segment whose extremities belong to the circle C and whose length is d, theta0 being the angle defining the first extremity (the sign of d tells what "first" means here... try it).
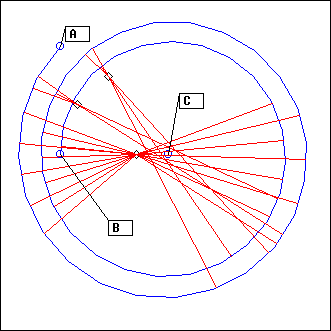
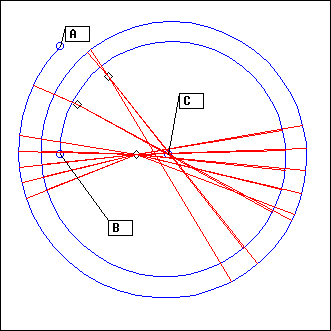
ArcC
L = ArcC(C, theta0, theta1, s, ...)
L = ArcC(C, A, B, s, ...)
C: circle
theta0, theta1: floats
A,B: points
s: 0, 1 or -1
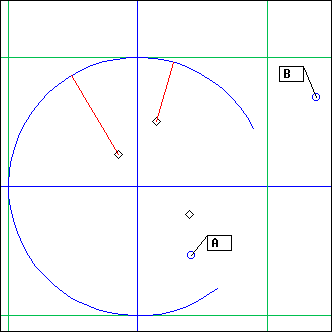ex: s = 1
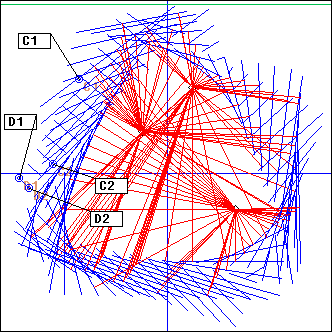
EcouteC() is performed on C, then its result is cropped to the part of the circle between angles theta0 and theta1 (or between the projections of points A and B). s gives the sense of rotation (1 clockwise, -1 counter-clockwise); if it is not present or 0, the shortest support will be selected.
Examples with the above setting (image):
ArcC(C1, A, B, 1) # only the event at the bottom is projected
ArcC(C1, A, B) # same thing
ArcC(C1, A, B, -1) # the two upper events are projected
ArcC(C1, Pi/8, 14*Pi/8, -1) # same thing
ArcC(C1, A, -Pi/4, -1) # same thing
EcPiste
L = EcPiste(P, dp, closeflag, ...)
P: piste
dp: integer
closeflag: 0 or 1
ex: dp = 1
ex: dp = 10
Ecoute() is called for each couple of consecutive points in P; if closeflag is 1, the last point is also linked to the first one.
If dp is more then one, Ecoute() is called on couples of points that are dp point away in the piste.
The nice piste you see in the example is a rose curve. You can have a look here to see how you can define a piste from a parametric formula; this one was created by the following command:
P = ParaPiste(0, 2*Pi, 0.01*Pi, Rose, 1, 3)
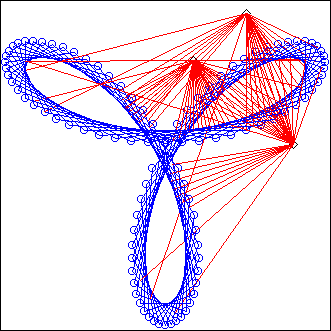
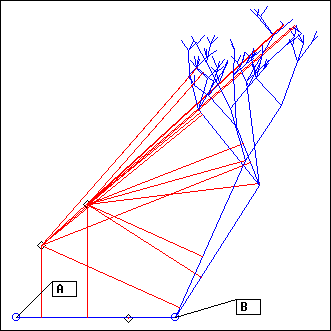
SpiralAB
L = SpiralAB(A, B, C, nT, nEc, ...)
A,B,C: points
nT, nEc: integers
ex: nT=2, nEc=50
ex: nT=2, nEc=100
The projector is a spiral of Ecoute() segments. The spiral goes from A to B, making nT rounds around its center C. It is divided in nEc segments.
nT can be positive or negative; this will set the direction of the spiral
The result is very much depending on the value for nEc. You should experiment with it to see how it behaves.
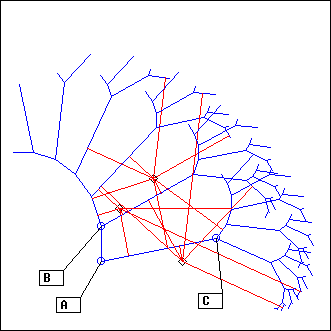
RandTree
L = RandTree(A, B, depth, nbmin, nbmax, thmin, thmax, lmin, lmax, scf, ...)
A, B: points
depth, nbmin, nbmax: integers
thmin, thmax, lmin, lmax, scf: float
ex: depth=5, nb = 3 to 5, scf = 0.8
Creates a random tree of Ecoute() segments.
AB is the first segment (the trunc). The following process is repeated depth times:
- from nbmin to nbmax new segments fork from the extremity of the trunc (B)
- their (absolute) angle ranges from thmin to thmax
- their length range from lmin to lmax
- the process is repeated for each new extremity, lmin and lmax being scaled by scf
All segments from the same depth are merged (mixed), then all mixes are added, starting with the trunc (which can be nil: A=B is allowed).
Be careful with this projector, as it may lead to very big lignes !
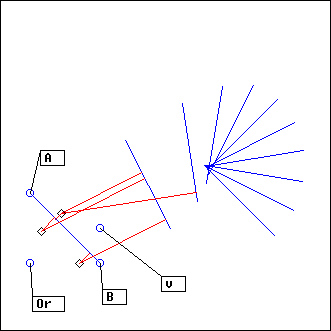
FractalV
L = FractalV(A, B, C, depth, dth1, dth2, lf1, lf2, ...)
A, B, C: points
depth: integer
dth1, dth2, lf1, lf2: float
ex: depth = 5, dth1= -0.1*Pi, dth2 = 0.2*Pi, lf1= 0.9, lf2= 0.5
The V-shaped pattern ABC is fractalised depth times: dth1 and dth2 are the angle increments for each extremity, lf1 and lf2 the length factors
As with RandTree, all segments from the same depth are merged, then the mixes are added.
Trying it is the best way to understand what it does. Be careful as it is very easy to create huge lignes with this projector.
FractalAB
L = FractalAB(A, B, depth, v, dth, lf, vdth, vlf, ...)
A,B,v: points/vector
depth: integer
dth,lf,vdth,vlf: floats
ex: depth=10, dth = 0.1*Pi, lf=1, vdth =-0.1*Pi, vlf = 0.5
Starting with the segment AB, the following process is repeated depth-1 times:
- a new segment is created by moving AB according to v (here, v is a vector: the "arrow" going from the origin (points x=0, y=0) to the point v is used to represent the motion of the segment).
- it is rotated by dth
- its length is scaled by lf
- v is rotated by vdth
- the length of v is scaled by vlf
Ecoute() is called on each segment; the resulting lignes are added
RandConnect
L = RandConnect(P, nEc, ...)
P: piste
nEc: integer
Ecoute() is called on nEc segments created from random points from P.
(The example picture uses the same piste as in EcPiste)
EarWalk, EarJump
L = EarWalk(P, len, d, speed, ...)
L = EarJump(P, len, d, beat, ...)
P: piste
len, beat: integer
speed: float
d: point or angle (float from 0 to 2*Pi)
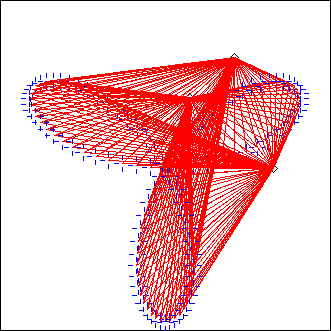
EcouteC() is called on each point in P: a circle centered on this point and of perimeter len (given in clicks !) is used, with starting point d. The overall duration is defined by the length of the piste, so the usual optional parameter duration has a different meaning here (or no meaning at all); instead, use speed to change the "tempo" (by default, speed = CPCM)
This projector has been intended to be used with a very small len (it can be 0), so that each circle behaves like a point listening to the whole scene at the same time; thus it is very sensitive to the distortion functions settings. You may think of it as a point navigating along the piste at speed speed and sampling the fields of distortions emanating from the events. There should be very few of them, or else the Volume distortion function should be decreasing to zero, or else you should add a region argument (in relative mode), since all events will sound together for each point of the piste (of course you can also set len to a higher value, in which case the events are separated, having at least a starting time offset; then it makes sense to play with the parameter d).
Also, note that the side effect is meaningless here. Each circle being scanned clock-wise, all events will always be projected from the left.
In a certain sense, EarWalk and EcPiste are complementary ways of listening to the scene along a piste.
EarJump is a variation on EarWalk where the distance between consecutive points is not considered: the corresponding EcouteC() calls are separated by a duration beat (optional, default being 1b)
Batteur
L = Batteur(name, program, ...)
name, program: strings
This complex projector has a dedicated page...
Polygon, ParaPolygon
L = Polygon(C, nC, th0, ...)
L = ParaPolygon(C, nC, th0, ...)
C: circle
nC: integer
th0: float
nC = 7, th0 = 0.2
nC = 20, th0 = 0
Ecoute() segment are arranged (added) to form a regular polygon with nC sides, its corners belonging to the circle C.
th0 is the starting angle on C.
The ParaPolygon version merges the segments instead of adding them.
TPol, TPPol
L = TPol(C, nC, th0, dth, nP,...)
L = TPPol(C, nC, th0, dth, nP,...)
C: circle
nC, nP: integers
th0, dth: floats
nC = 4, dth = 0.01*Pi, nP = 10
TPol stands for "T"urnig "Pol"ygon:
the first three arguments describe a Polygon, which is rotated nP times, dth being the angular increment.
If nP is omitted or 0, it is set automatically to nP = 2*Pi/(nC*dth)
TPPol is the same as TPol, apart from the fact that it calls ParaPolygon instead of Polygon
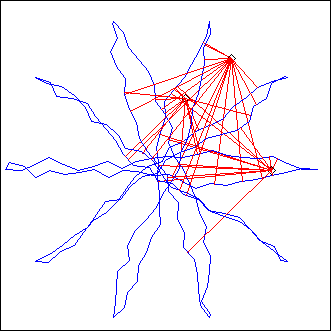
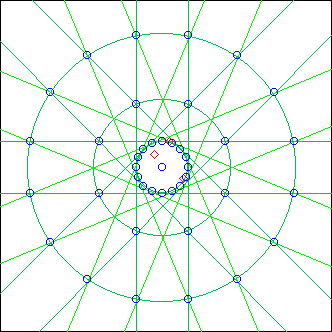
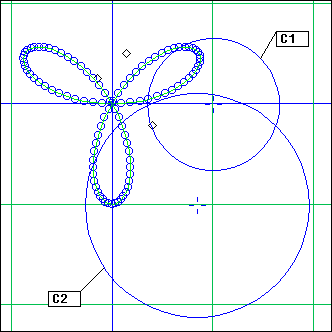
MultiP
L = MultiP(p, projcall)
p: piste
projcall: string
(no usual optional arguments, only a closure)
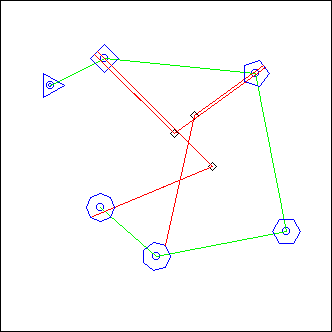
This is a metaprojector (like MetaPars, MetaRails, TDiam)
projcall is called for each point P_ in the piste p.
The resulting lignes are merged, so this is a way to process projections in parallel.
The integer value N_ can be used in projcall: it is the index of P_ in the p array.
Example: in the above image we used
projcall = "Polygon(Cerc(P_, 0.2), N_+2, 0)"
(the piste appears in green)
RBox
L = RBox(pA, pB, pO, pD, dur, dth, ...)
pA, pB, pO, pD: points
dur: integer
dth: float
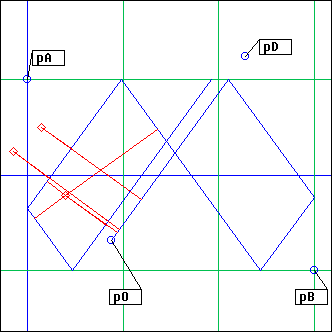dur = 2000, dth = 0
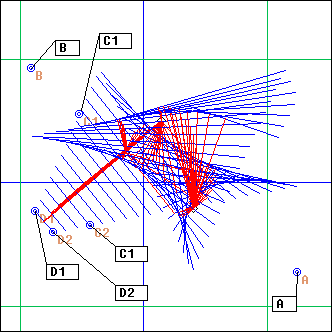dur = 2000, dth = 0.01
This is a billiard game: pA and pB are opposite corners of the billiard table; the ball is initially in pO and targets pD (pD can also be an angle value, from 0 to 2*Pi)
The projection stops after a duration dur has been reached.
The optional dth argument is added to the bounce angle for each new segment.
(here is an example composition based on RBox)
CBox
L = CBox(C, pO, pD, dur, dth, ...)
C: cercle
pO, pD: points
dur: integer
dth: float
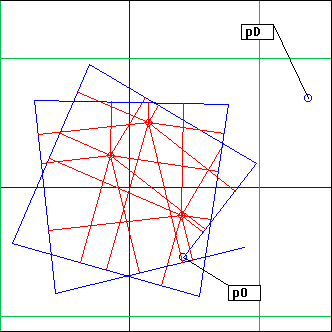dur = 2000, dth = 0
Same as above... this is a circular billiard game. The starting point pO must be inside the circle C; pD can be anywhere.
Goutte
L = Goutte(A, B, d, prog, ...)
A, B: points
d: float
prog: array or string
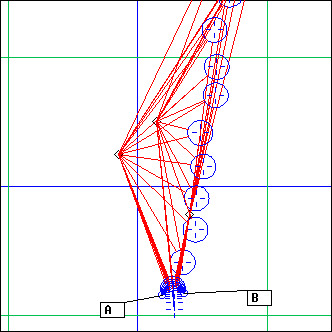
A number of ArcCs whose extremities are A and B are added; prog and d defines the ArcCs parameters
d gives the unit of distance to consider on the line perpendicular to AB and going through its middle; prog lists the distances of the circle centers for the ArcCs supports. They can be positive or negative.
If d is 0, it is set to Dist(A,B).
prog can either be a string, like
"1,2,3,-10,-5,0"
... or an array, like
[1=1, 2=2, 3=3, 4=-10, 5=-5, 6=0]
Bulle
L = Bulle(A, B, param, ...)
A, B: points
param: array
(zoom)
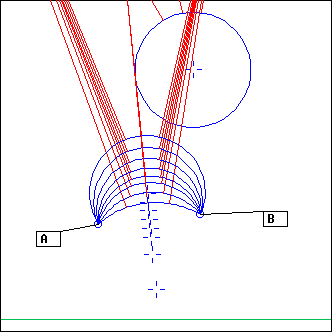
A and B define the mouth of a bubble gun; param is an array of parameters used to customize it.
The idea is the following: a number of growing ArcCs whose extremities are A and B is followed by a random number of EcouteCs whose supports are moving away from the mouth AB. All of this projectors are added. Here are the possible parameters:
- "-N" is the number of ArcCs. The larger it is, the larger is the eventual bubble diameter
- "N" is the maximum number of EcouteCs
- "Nmin" is the minimum number of EcouteCs
- "dxu" is the amplitude of the bubble motion away from the gun
- "dyu" is the amplitude of the random offsets parallel to the mouth of the gun (the segment AB)
... note that both "dxu" and "dyu" are relative to the bubble diameter
- "v" is a sort of wind: it is a vector that will be added to the bubble position at each motion step
param may contain any subset of such parameters, or all of them; the missing parameters are replaced by defaul values, so that giving []
as param is the same as giving
["-N"= 8; "N"= 20; "Nmin"= 2, "dxu"= 2, "dyu"= 2, "v"=["x"=0,"y"=0]]
LinInv
L = LinInv(pref, dp, C1, C2, nC, ...)
pref: piste
dp, nC: integers
C1, C2: circles
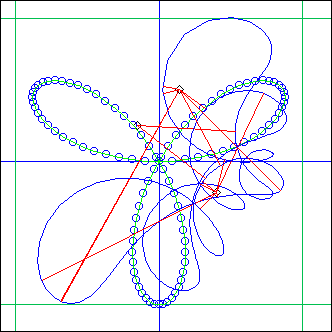
nC circles are defined between C1 and C2 (like in the Onde projector); the reference piste pref is inverted with respect to each of these circles, and EcPiste is called nC times, with arguments the inverted piste and dp. All results are added.
SpirInv
L = SpirInv(pref, dp, C, radius, th0, dth, nC, ...)
pref: piste
dp, nC: integers
C: circle
radius, th0, dth: floats
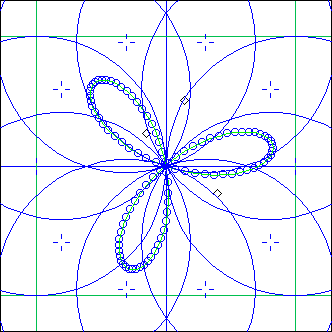the reference piste and 10 circles
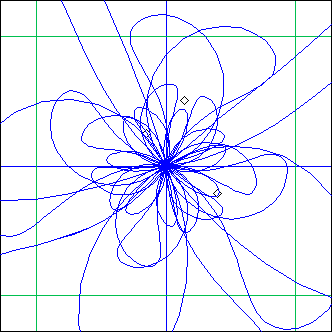the resulting supports
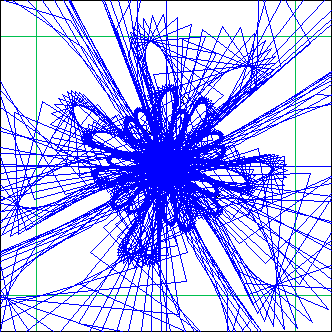same thing with dp=10
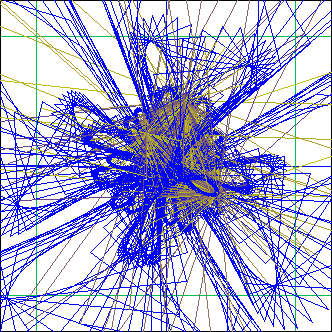... makes a lot of projections !
Same thing as previously, but this time the circles used for inversion are defined like in the Spiro projector.
Segments
L = Segments(aS, ...)
aS: array
Apply EcouteS() on all elements in array aS. The results are added according to the index order.
Such elements should be segments, obviously. However note that the optional element indexed 0 is skipped, along with all elements whose TypeOf() is not array:xy4
Cercles
L = Cercles(aC, A, nT, ...)
aC: array
Apply EcouteC() on all elements in array aC. The results are added according to the index order.
Such elements should be circles. Note that the optional element indexed 0 is skipped, along with all elements whose TypeOf() is not array:circle
ADrummer
L = ADrummer(fop, d, nS, param, ...)
fop: point
d: float
nS: integer
param: array
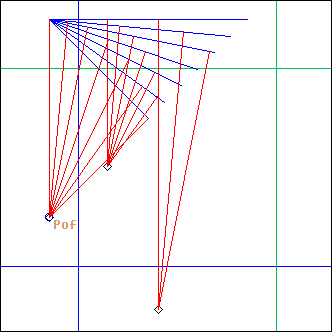nS = 7
This is a specific kind of Echelle() projection, where the segments are organised so that point pof always gets projected on them, at the beginning of the first segment, and at the end of the last one. d sets the distance between pof and its first projection. nS is the number of segments.
The distortion functions of type Volume, Pit and Time are defined by the projector itself. This settings and a couple of geometrical parameters are defined by the param argument, an array of parameters. This is not documented here since it is subject to changes and improvements. Please refer directly to the code for details...
See also ADMorph.
ADMorph
L = ADMorph(fop, d, nS, param1, param2, pattern, ...)
fop: point
d: float
nS: integer
param1, param2: arrays
pattern: phrase
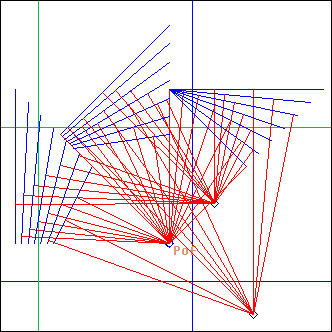nS = 7, pattern = ´a,a,a´
An arrangement of several ADrummers following a pattern. Each note in the pattern is replaced by the corresponding projection. The param argument of ADrummer is morphed from param1 to param2, (see the documentation of ArrMorph() for details)
(Note: ADMorph & ADrummer have been designed with the aim of providing a flexible way to compose tabla-like rythmic patterns)
PolyMorph
L = PolyMorph(c1, nC1, th1, c2, nC2, th2, nP, ...)
c1, c2: circles
th1,th2: floats
nC1, nC2, nP: integers
c1=c2, th1=th2=0, nC1=3, nC2=10, nP=10
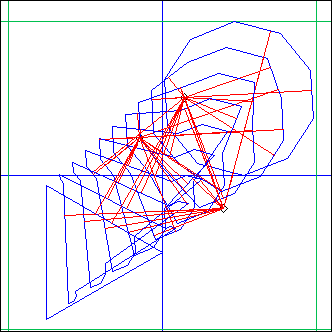here c1!=c2, th1=0, th2=1
This computes a morphing between Polygon(c1, nC1, th1, ...) and Polygon(c2, nC2, th2, ...) in nP steps. The polygons are added.
Hear an example here.
OscBeat
L = OscBeat(a, b, amp, mode, nS, nCY, offset, ...)
a, b: points
amp: float
mode, nS, nCy, offset: integers
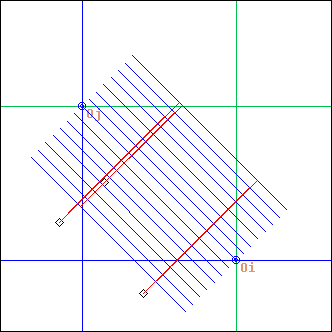a=Oi, b=Oj, amp=0.5, mode=1 (linear), nS=15, offset=0
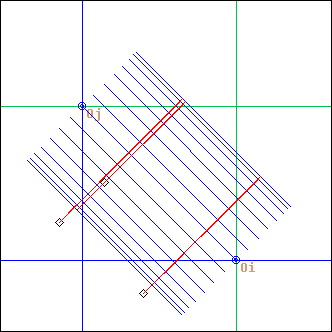same here with mode=2 (sinusoid)
OscBeat stands for "osc"illating "beat"
Ecoute() is performed nS times with supports described by a segment initially at a,b and oscillating around this position with an amplitude amp. The projections are added.
mode sets the oscilation mode: either linear (1), sinusoidal (2) or in x^2 (3). The sinusoidal mode spends more time near the amplitude extremums, while the x^2 mode spends more time around the initial position.
nCy sets the number of oscillation cycles (default is 1), while offset (an integer interpreted modulo nS, and defaulting to 0) allows the oscillation to be dephased, that is to start elsewhere than in segment a,b.
MetaPhrase
L = MetaPhrase(ph, projcalls)
ph: phrase
projcalls: array
(no usual optional arguments, only a closure)
(more here later ...)
MetaPhraseAB
L = MetaPhraseAB(ph, projcalls, P1, P2)
ph: phrase
projcalls: array
P1, P2: pistes
(no usual optional arguments, only a closure)
(more here later ...)
CDeMul
L = CDeMul(pinit, projcall, ...)
pinit: point
projcall: string (a projector call)
This is a bizarre meta-projector based on MetaRails. projcall is first evaluated with "A_" being replaced with point pinit. The resulting phrase is then used to define a piste, and MetaRails is called with projcall on this piste (both for A_ and B_).
Here is how the piste is computed: each note of the phrase gives birth to a point on a circle centered on pinit and of length the phrase length. The angle of the point (from 0 to 2*Pi) is proportional to the time attribute of the note (from 0 to the length of the phrase)
RollOnPiste
L = RollOnPiste(pst, maxp, ...)
pst: piste
maxp: float
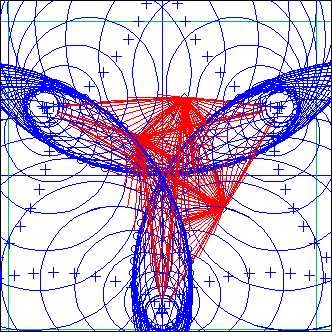
EcouteC() is performed on a set of circles built by taking each point in piste pst and calculating the circle passing through this point and the two following ones. If that circle perimeter is greater than maxp, the circle is skipped (unless maxp is 0, which is the default).
The projections are added.
Rayons
L = Rayons(pA, pst, ...)
pA: point
pst: piste
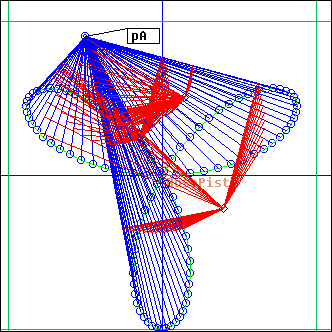
Ecoute is performed on the set of segments linking point pA and all points defining piste pst. Projections are added.
PWeb
L = PWeb(pA, pB, dla, dlb, len, ...)
pA, pB: pistes
dla, dlb, len: floats
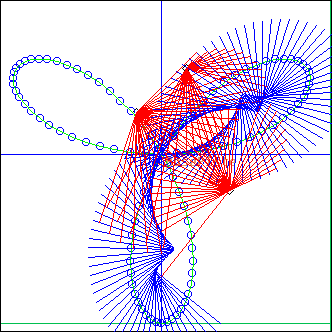
Ecoute is performed on segments linking points in piste pA to points in piste pB.
The points start at the beginning of the pistes, then proceed along the pistes by steps dla and dlb.
The projection stops when the ligne duration gets longer than len
RBox2, CBox2
L = RBox2(pA, pB, pO1, dir1, pO2, dir2, dla, dlb, dur, dtha, dthb, ...)
L = CBox2(cer, pO1, dir1, pO2, dir2, dla, dlb, dur, dtha, dthb, ...)
cer: circle
pA, pB, pO1, pO2: points
dir1, dir2: angles or points
dla, dlb, dtha, dthb: floats
dur: integer
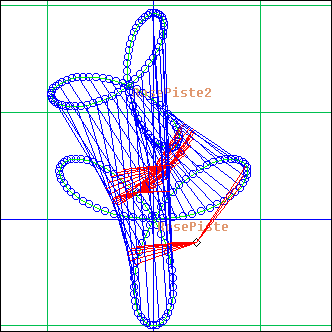
In these projectors we use two RBox or CBox trajectories as pistes arguments for a PWeb call.
The parameters are a mix of RBox/CBox arguments and PWeb arguments.
PHelice
L = PHelice(pst, dl, dia, th0, dth, len, ...)
pst: piste
pst, dl, dia, th0, dth, len: floats
An Helice of diameter dia which center moves along the piste pst, by steps of dl.
The projection stops when the ligne duration gets longer than len.
Radar
L = PHelice(cir, d, th0, dth, nseg, ...)
cir: circle
th0, dth: floats or points
d: float
nseg: integer
(more here later ...)
RadarScan
L = PHelice(cir, d, th0, dth, nseg, ...)
cir: circle
th0, dth: floats or points
d: float
nseg: integer
(more here later ...)
-- Back --